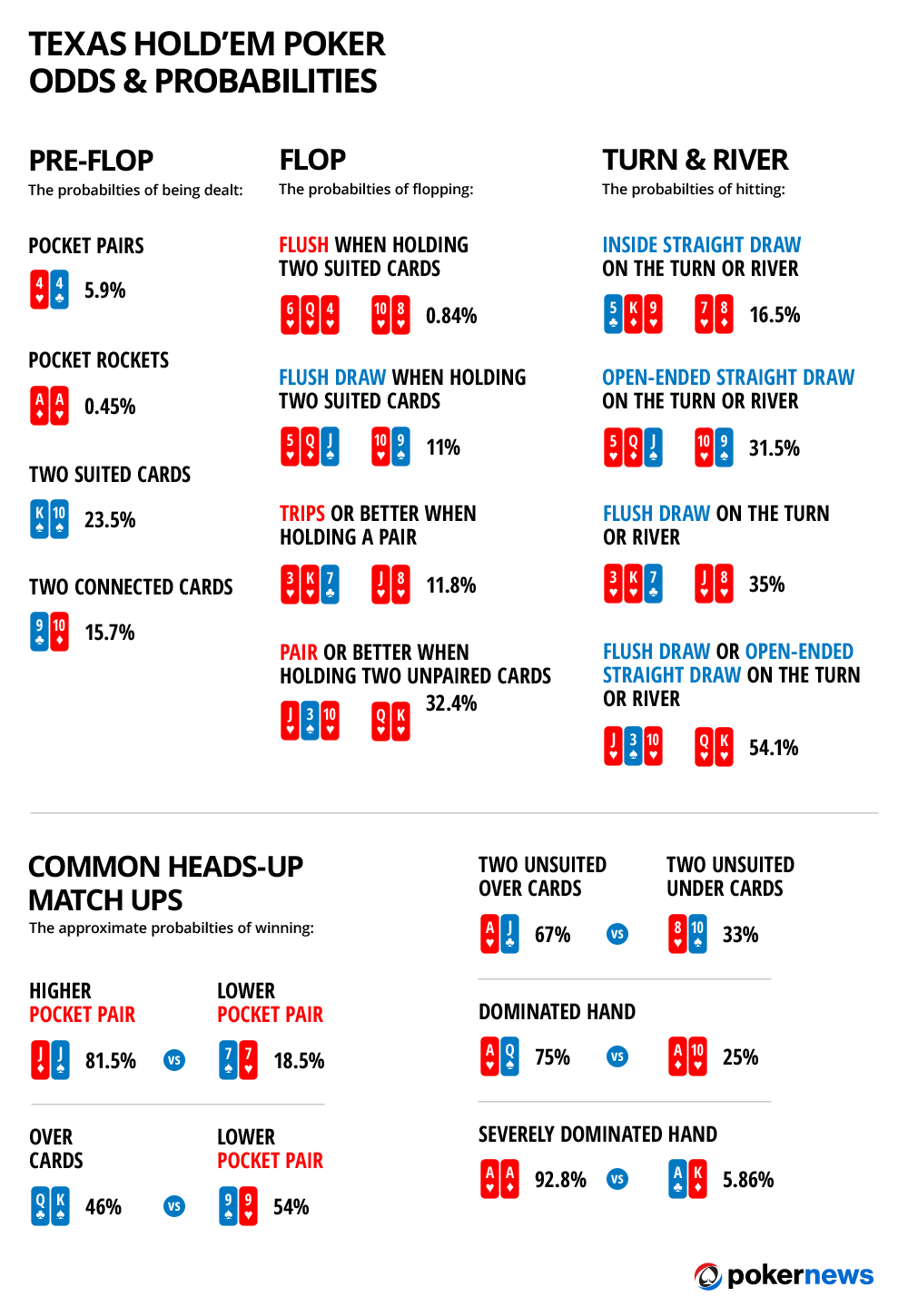
Poker Hands Order Odds
All that said there are hands that have significantly better odds. In general big pocket pairs like pocket aces, kings and queens dominate the rest of the starting hands. We’ve compiled a list of the best starting hands in Hold’em below, which should provide a solid framework for beginner and intermediate poker.
NL Hold’em Starting Hand Charts
The hands are listed in descending order of probability, which could be used as the basis for their ranking order in multi-deck poker variations. It can be seen that as the number of decks increases, flushes become easier to make than straights, and sets of equal cards become more common. These are the same hand. Order is not important. The number of possible 5-card poker hands would then be the same as the number of 5-element subsets of 52 objects. The following is the total number of 5-card poker hands drawn from a standard deck of 52 cards. Official Poker Hand Rankings Know your poker hand order. A poker hand consists of five cards, which fall into several categories. Below is the complete list of poker hands, from highest to lowest. Please note that hand rankings for Short Deck are slightly different. Find out more about the short deck poker hand rankings on the dedicated page. The Science Behind Odds of a Hand Your chances of getting any two cards of different values but specific suits as in 10s 4c (regardless of the order in which they are dealt), on the other hand, are 1/1,326. Here’s the math behind it: P = 1/52 x 1/51 (because you’re getting one card and then one more future card).
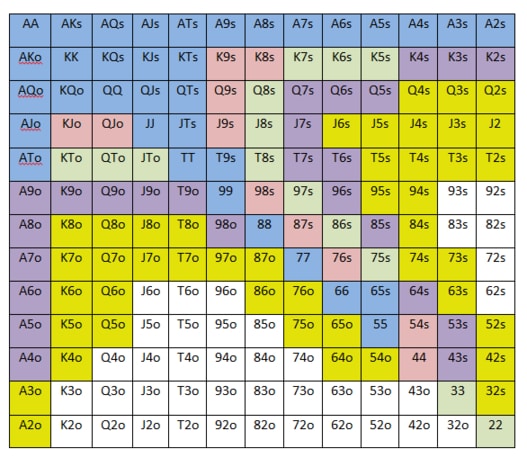
One aspect of the game of No-Limit Hold’em that causes beginning players much grief is deciding which hands to play and which hands to dump. NL Hold’em is much more difficult than Limit Hold’em because the value of a hand depends on so many factors other than just the cards in your hand. Despite this difficulty, our coaches believe that following some general guidelines and adjusting from these is a better solution than having no guidelines at all. Given that well over half of your profitability in NL Hold’em is based on hand selection alone, we have developed these charts to help you better determine whether to play or fold.
There are no perfect No-Limit starting hand charts. That is because there are many factors that affect your decision, and charts cannot account for all of them. Some of these include:
- The size of your opponent's stacks.
- How loose or tight, passive or aggressive, your opponents are.
- Where these opponents are located at the table – for example, does an aggressive player still have to act after you?
- Your image at the table – for example, how tight or tricky you are perceived.
That being said, these charts will serve you well in most typical low-stakes No-Limit cash games, such as games with blinds of $1/$2, and home games. These games typically have several loose players at the table, and good opportunities for winning big pots with suited connectors and pocket pairs. With practice, you will be able to be a consistently winning player with these charts as a starting point. As you improve, you'll find yourself making adjustments to these charts based on the factors listed above, and more.
AGAIN: These charts are a good starting point for beginners. Specifically, Chart #1 recommends a significant amount of limping. This is great in loose, passive games but less often seen in tougher games. You’ll find other training material on Advanced Poker Training that may recommend a more aggressive approach for more experienced players.
Note: It would be a serious mistake to apply these hand charts before reading the Frequent Asked Questions first.
CHART #1 ‐ LOOSE, PASSIVE GAME (OFTEN 4-5 LIMPERS PER HAND)
NO ONE HAS RAISED YET
- Raise Always
- Call from Early Position, otherwise raise
- Call always
- Call from Middle or Late Position if the conditions are right (see Frequently Asked Questions)
CHART #2 ‐ TIGHTER GAME (FEWER LIMPERS) OR MORE AGGRESSIVE GAME
NO ONE HAS RAISED YET
- Raise Always
- Call from Early Position, otherwise raise
- Call (or Raise) from Middle or Late Position if the conditions are right (see Frequently Asked Questions)
CHART #3 ‐ THERE HAS BEEN A SINGLE RAISE
(3‐5 TIMES THE BIG BLIND) BEFORE YOU
- Re‐Raise Always
- Call from Early Position, otherwise re‐raise
- Call always
- Call from Middle or Late Position if the conditions are right (see Frequently Asked Questions)
FREQUENTLY ASKED QUESTIONS
For the hands in yellow, what do you mean when you say to play these hands if the conditions are right? The hands in yellow are speculative hands. They should always be folded from Early Position. From other positions, they can be profitable given the right conditions. Some of the questions to ask yourself:
- Are there other players who have called so far (the more, the better)?
- Are the players who have called playing poorly after the flop? Will they pay me off if I hit something?
- Is there an aggressive player still to act behind me (you might get raised and have to fold)?
- If there has been a raise and no other callers, what chance do I have of using my position after the flop to win the hand even if I don't improve (Chart #3 only)?
Why does Chart #2 say to sometimes raise with the hands in yellow, but Chart #1 does not? We have different goals in mind. Using Chart #1, we want to call to encourage additional players to enter the pot. These hands will be immensely profitable when our loose, passive opponents enter the hand, and get trapped when we flop a set, or make a well-disguised straight. When using Chart #2, however, we want to size up the opponents still to act. If they are tight, we can raise. Sometimes, we'll pick up the blinds. Other times, our pre-flop aggression will allow us to take down the pot on the flop.
What's the difference between AKs and AKo? AKs means an Ace and King of the same suit. AKo means an Ace and King of different suits.
What are early, middle, and late position? Early Position is generally the first 2 (in a nine player game) or 3 (in a ten player game) positions after the blinds. Late Position is the “cutoff” position (to the right of the dealer), and dealer button positions. Middle Position is everything in between.
How much should I raise? As a general rule, raise 3 to 4 times the big blind, plus 1 extra big blind for every player who has called before you. So if there are 2 callers already, raise between 5 and 6 times the big blind.
What if someone raises after I call? Whether you call the raise depends on how much money the raiser has for you to win, how many other players are involved, and what type of hand you have. As a general rule, if you have a pocket pair, lean towards calling. If there are a lot of other players (and therefore a big pot), lean towards calling. In general, fold suited connectors from early position. Fold hands like KQ that don't play well against a raiser.
How do I play from the blinds? From the small blind, play the same hands you would play from late position, plus a few more. But don't call with junk hands like T5o, just because it is “cheap”. From the big blind, if there is a raise to you, play like you would if you had already called from early position.
The chart says to fold KQo to a raise. Really? Yes, this hand performs very poorly against typical raising hands. Against AK, AQ, AA, KK, QQ, you are a big underdog. Other typical raising hands like JJ, TT, 99, AJs, are slightly ahead of you as well. The only time you might call or re-raise is from late position, if the opener was in middle or late position, indicating they might have a wider range of hands.
I was told to fold AJo from Early Position, why do you say to call with it? Folding AJo is not a bad idea in many games. We included it because, at low stakes tables (even tight or aggressive ones), the players are often playing badly enough after the flop that it can be profitable. We used data from millions of hands of low-limit poker to analyze this. The same could be said for KQo, ATs, and KJs – you can make a small profit in the long run at most low-stakes games, but folding would be perfectly acceptable from early position.
Can I use these charts in a NL Hold'em tournament? The charts would be best applicable to the early stages of a NL tournament, when everyone has a deep stack. In the middle and later stages, they should not be used.
Read all our instructional articles
This post works with 5-card Poker hands drawn from a standard deck of 52 cards. The discussion is mostly mathematical, using the Poker hands to illustrate counting techniques and calculation of probabilities
Working with poker hands is an excellent way to illustrate the counting techniques covered previously in this blog – multiplication principle, permutation and combination (also covered here). There are 2,598,960 many possible 5-card Poker hands. Thus the probability of obtaining any one specific hand is 1 in 2,598,960 (roughly 1 in 2.6 million). The probability of obtaining a given type of hands (e.g. three of a kind) is the number of possible hands for that type over 2,598,960. Thus this is primarily a counting exercise.
___________________________________________________________________________
Preliminary Calculation
Usually the order in which the cards are dealt is not important (except in the case of stud poker). Thus the following three examples point to the same poker hand. The only difference is the order in which the cards are dealt.
These are the same hand. Order is not important.
The number of possible 5-card poker hands would then be the same as the number of 5-element subsets of 52 objects. The following is the total number of 5-card poker hands drawn from a standard deck of 52 cards.
The notation is called the binomial coefficient and is pronounced “n choose r”, which is identical to the number of -element subsets of a set with objects. Other notations for are , and . Many calculators have a function for . Of course the calculation can also be done by definition by first calculating factorials.
Thus the probability of obtaining a specific hand (say, 2, 6, 10, K, A, all diamond) would be 1 in 2,598,960. If 5 cards are randomly drawn, what is the probability of getting a 5-card hand consisting of all diamond cards? It is
This is definitely a very rare event (less than 0.05% chance of happening). The numerator 1,287 is the number of hands consisting of all diamond cards, which is obtained by the following calculation.
The reasoning for the above calculation is that to draw a 5-card hand consisting of all diamond, we are drawing 5 cards from the 13 diamond cards and drawing zero cards from the other 39 cards. Since (there is only one way to draw nothing), is the number of hands with all diamonds.
If 5 cards are randomly drawn, what is the probability of getting a 5-card hand consisting of cards in one suit? The probability of getting all 5 cards in another suit (say heart) would also be 1287/2598960. So we have the following derivation.
Thus getting a hand with all cards in one suit is 4 times more likely than getting one with all diamond, but is still a rare event (with about a 0.2% chance of happening). Some of the higher ranked poker hands are in one suit but with additional strict requirements. They will be further discussed below.
Another example. What is the probability of obtaining a hand that has 3 diamonds and 2 hearts? The answer is 22308/2598960 = 0.008583433. The number of “3 diamond, 2 heart” hands is calculated as follows:
One theme that emerges is that the multiplication principle is behind the numerator of a poker hand probability. For example, we can think of the process to get a 5-card hand with 3 diamonds and 2 hearts in three steps. The first is to draw 3 cards from the 13 diamond cards, the second is to draw 2 cards from the 13 heart cards, and the third is to draw zero from the remaining 26 cards. The third step can be omitted since the number of ways of choosing zero is 1. In any case, the number of possible ways to carry out that 2-step (or 3-step) process is to multiply all the possibilities together.
___________________________________________________________________________
The Poker Hands
Here’s a ranking chart of the Poker hands.
The chart lists the rankings with an example for each ranking. The examples are a good reminder of the definitions. The highest ranking of them all is the royal flush, which consists of 5 consecutive cards in one suit with the highest card being Ace. There is only one such hand in each suit. Thus the chance for getting a royal flush is 4 in 2,598,960.
Royal flush is a specific example of a straight flush, which consists of 5 consecutive cards in one suit. There are 10 such hands in one suit. So there are 40 hands for straight flush in total. A flush is a hand with 5 cards in the same suit but not in consecutive order (or not in sequence). Thus the requirement for flush is considerably more relaxed than a straight flush. A straight is like a straight flush in that the 5 cards are in sequence but the 5 cards in a straight are not of the same suit. For a more in depth discussion on Poker hands, see the Wikipedia entry on Poker hands.
The counting for some of these hands is done in the next section. The definition of the hands can be inferred from the above chart. For the sake of completeness, the following table lists out the definition.
Definitions of Poker Hands
| Poker Hand | Definition | |
|---|---|---|
| 1 | Royal Flush | A, K, Q, J, 10, all in the same suit |
| 2 | Straight Flush | Five consecutive cards, |
| all in the same suit | ||
| 3 | Four of a Kind | Four cards of the same rank, |
| one card of another rank | ||
| 4 | Full House | Three of a kind with a pair |
| 5 | Flush | Five cards of the same suit, |
| not in consecutive order | ||
| 6 | Straight | Five consecutive cards, |
| not of the same suit | ||
| 7 | Three of a Kind | Three cards of the same rank, |
| 2 cards of two other ranks | ||
| 8 | Two Pair | Two cards of the same rank, |
| two cards of another rank, | ||
| one card of a third rank | ||
| 9 | One Pair | Three cards of the same rank, |
| 3 cards of three other ranks | ||
| 10 | High Card | If no one has any of the above hands, |
| the player with the highest card wins |
___________________________________________________________________________
Counting Poker Hands
Straight Flush
Counting from A-K-Q-J-10, K-Q-J-10-9, Q-J-10-9-8, …, 6-5-4-3-2 to 5-4-3-2-A, there are 10 hands that are in sequence in a given suit. So there are 40 straight flush hands all together.
Four of a Kind
There is only one way to have a four of a kind for a given rank. The fifth card can be any one of the remaining 48 cards. Thus there are 48 possibilities of a four of a kind in one rank. Thus there are 13 x 48 = 624 many four of a kind in total.
Full House
Let’s fix two ranks, say 2 and 8. How many ways can we have three of 2 and two of 8? We are choosing 3 cards out of the four 2’s and choosing 2 cards out of the four 8’s. That would be = 4 x 6 = 24. But the two ranks can be other ranks too. How many ways can we pick two ranks out of 13? That would be 13 x 12 = 156. So the total number of possibilities for Full House is
Note that the multiplication principle is at work here. When we pick two ranks, the number of ways is 13 x 12 = 156. Why did we not use = 78?
Flush
There are = 1,287 possible hands with all cards in the same suit. Recall that there are only 10 straight flush on a given suit. Thus of all the 5-card hands with all cards in a given suit, there are 1,287-10 = 1,277 hands that are not straight flush. Thus the total number of flush hands is 4 x 1277 = 5,108.
Straight
There are 10 five-consecutive sequences in 13 cards (as shown in the explanation for straight flush in this section). In each such sequence, there are 4 choices for each card (one for each suit). Thus the number of 5-card hands with 5 cards in sequence is . Then we need to subtract the number of straight flushes (40) from this number. Thus the number of straight is 10240 – 10 = 10,200.
Three of a Kind
There are 13 ranks (from A, K, …, to 2). We choose one of them to have 3 cards in that rank and two other ranks to have one card in each of those ranks. The following derivation reflects all the choosing in this process.
Two Pair and One Pair
These two are left as exercises.
Poker Hands Order Of Strength
High Card
The count is the complement that makes up 2,598,960.
The following table gives the counts of all the poker hands. The probability is the fraction of the 2,598,960 hands that meet the requirement of the type of hands in question. Note that royal flush is not listed. This is because it is included in the count for straight flush. Royal flush is omitted so that he counts add up to 2,598,960.
Probabilities of Poker Hands
Poker Odds And Outs
| Poker Hand | Count | Probability | |
|---|---|---|---|
| 2 | Straight Flush | 40 | 0.0000154 |
| 3 | Four of a Kind | 624 | 0.0002401 |
| 4 | Full House | 3,744 | 0.0014406 |
| 5 | Flush | 5,108 | 0.0019654 |
| 6 | Straight | 10,200 | 0.0039246 |
| 7 | Three of a Kind | 54,912 | 0.0211285 |
| 8 | Two Pair | 123,552 | 0.0475390 |
| 9 | One Pair | 1,098,240 | 0.4225690 |
| 10 | High Card | 1,302,540 | 0.5011774 |
| Total | 2,598,960 | 1.0000000 |
Poker Hand Odds Calculator
___________________________________________________________________________
2017 – Dan Ma